Persamaan Garis Singgung Lingkaran II

Persamaan Garis Singgung Lingkaran II

Posted on 27 November 2013 by yos3prens

Pada pembahasan ini, kita akan menentukan persamaan garis singgung lingkaran yang melalui titik A(x₁, y₁) pada lingkaran yang berpusat di titik (a, b) dan berjari-jari r. Seperti kita ketahui, persamaan lingkaran yang berpusat di titik (a, b) dan berjari-jari r adalah (x – a)² + (y – b)² = r². Karena titik (x₁, y₁) terletak pada lingkaran maka,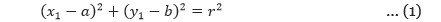

Untuk mengetahui ilustrasi mengenai letak garis singgung terhadap lingkaran tersebut, perhatikan ilustrasi berikut.

Apabila kita membuat ruas garis PA, yaitu jari-jari dari lingkaran P, maka gradien dari ruas garis tersebut adalah

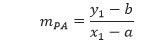
Karena ruas garis PA merupakan jari-jari yang memiliki salah satu titik ujung di titik A, yaitu titik yang juga dilalui oleh garis singgung k, maka ruas garis PA tegak lurus dengan garis k. Hal ini mengakibatkan,

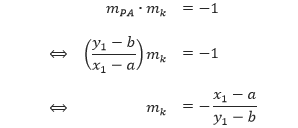
Karena garis k melalui titik A(x₁, y₁) dan bergradien m_k = –(x₁ – a)/(y₁ – b), maka persamaan garis k adalah

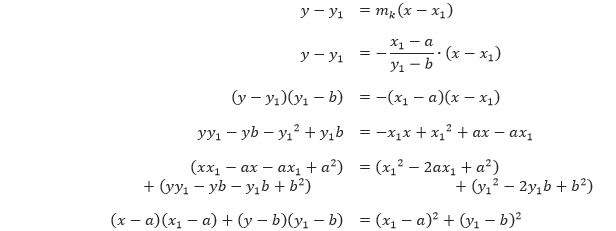
Apabila kita mensubstitusikan persamaan (1) ke dalam persamaan di atas, maka kita akan memperoleh,

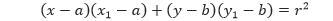
Sehingga, dari penghitungan di atas kita dapat menyimpulkan persamaan garis singgung yang kita peroleh adalah sebagai berikut.

Persamaan Garis Singgung Lingkaran
Persamaan garis singgung lingkaran yang melalui titik (x₁, x₂) pada lingkaran (x – a)² + (y – b)² = r² adalah,
(x – a)(x₁ – a) + (y – b)(y₁ – b) = r².

Selanjutnya, perhatikan contoh permasalahan mengenai garis singgung lingkaran (x – a)² + (y – b)² = r² berikut.
Contoh 1: Persamaan Garis Singgung Lingkaran
Tentukan persamaan garis singgung di titik (2, 4) pada lingkaran (x + 4)² + (y – 5)² = 37.
Pembahasan Lingkaran yang memiliki persamaan (x + 4)² + (y – 5)² = 37 memiliki titik pusat di (a, b) = (–4, 5) dan kuadrat jari-jarinya, r² = 37. Sehingga persamaan garis singgung yang melalui titik (x₁, y₁) = (2, 4) pada lingkaran tersebut adalah

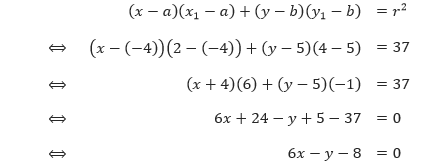
Sehingga, persamaan garis singgung lingkaran tersebut adalah 6x – y – 8 = 0.
Selanjutnya bagaimana kalau persamaan lingkarannya tidak ditulis ke dalam bentuk (x – a)² + (y – b)² = r², tetapi ke dalam bentuk persamaan umum lingkaran. Perhatikan contoh soal selanjutnya berikut.
Contoh 2: Garis Singgung untuk x² + y² + Ax + By + C = 0
Carilah persamaan garis singgung pada lingkaran x² + y² – 6x + 2y – 3 = 0 di titik yang berabsis 5.
Pembahasan Pertama, kita ubah persamaan x² + y² – 6x + 2y – 3 = 0 menjadi bentuk (x – a)² + (y – b)² = r².

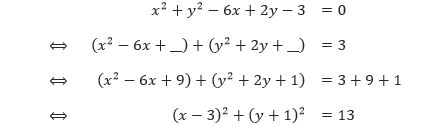
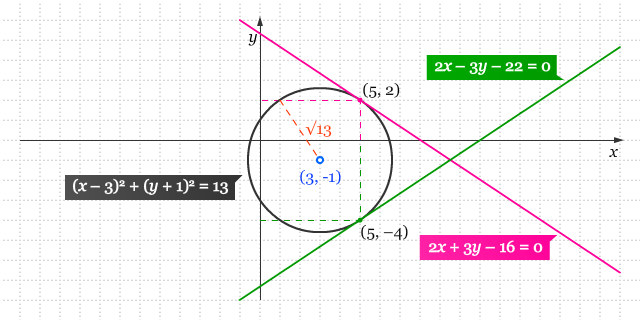
Sehingga, lingkaran tersebut memiliki titik pusat di (a, b) = (3, –1) dan kudrat dari jari-jarinya r² = 13. Selanjutnya kita tentukan titik pada lingkaran tersebut yang berabsis 5. Untuk x = 5, kita memperoleh

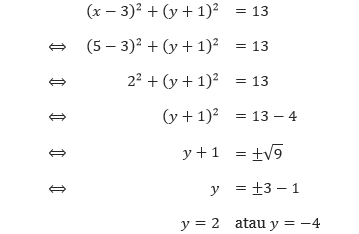
Sehingga, titik-titik pada lingkaran tersebut yang berabsis 5 adalah (5, –4) dan (5, 2). Diperoleh, persamaan garis singgung yang melalui titik (5, –3) adalah

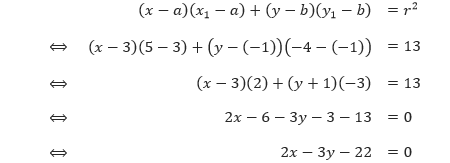
Sedangkan persamaan garis singgung yang melalui titik (5, 2) adalah

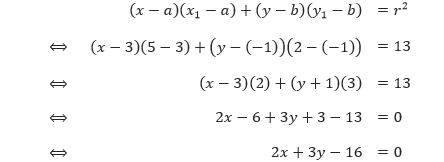
Jadi, persamaan garis-garis singgungnya adalah 2x – 3y – 22 = 0 dan 2x + 3y – 16 = 0. Perhatikan gambar dari dua garis singgung tersebut.

Irisan Kerucut

Irisan Kerucut

 

Posted on 11 Desem

ber 2013 by yos3prens

Rumus jarak, jarak titik dengan titik dan jarak titik dengan garis, dapat digunakan untuk menentukan persamaan dari kurva-kurva irisan kerucut. Tetapi sebelum menentukan persamaan-persamaan tersebut, kita akan membahas beberapa keluarga kurva yang dihasikan oleh irisan kerucut. Topi ulang tahun merupakan salah satu contoh kerucut yang dapat dijumpai di sekitar kita. Titik pada kerucut disebut titik puncak dan lembaran kertas yang membentuk sisi kerucut disebut selimut kerucut. Sesuai dengan namanya kurva-kurva dalam keluarga irisan kerucut, dapat dihasilkan dengan mengiris suatu kerucut, atau lebih tepatnya, kurva-kurva tersebut merupakan hasil perpotongan suatu bidang dengan kerucut. Apabila bidang tersebut tidak melalui titik puncak, irisannya akan menghasilkan lingkaran, elips, parabola, dan hiperbola. Perhatikan gambar berikut.

Masing-masing irisan kerucut tersebut dapat didefinisikan dalam persamaan jarak titik dengan titik, ataupun jarak titik dengan garis. Misalnya, titik-titik (–4, –2), (4, –2), dan (4, 4) merupakan titik-titik yang berada pada lingkaran yang berpusat di (0, 1) dan berjari-jari 5 satuan. Sehingga, definisi lingkaran adalah himpunan semua titik yang memiliki jarak yang sama (yang disebut jari-jari) terhadap suatu titik tertentu (yang disebut titik pusat).
Contoh lainnya, titik-titik (0, 0), (4, 2) dan (8, 8) yang dilalui oleh suatu parabola memiliki jarak yang sama terhadap titik (0, 2) dan garis y = –2. Ilustrasi ini mengarahkan kita ke dalam definisi parabola: parabola adalah himpunan semua titik yang memiliki jarak yang sama terhadap suatu titik tertentu (yang disebut titik fokus) dan suatu garis yang diberikan (yang disebut garis direktris).
Contoh : Menemukan Persamaan Parabola
Tentukan persamaan parabola yang memuat semua titik yang berjarak sama terhadap titik (0, 2) dan garis y = –2.

Pembahasan Kita gunakan pasangan berurutan (x, y) untuk merepresentasikan sembarang titik pada parabola. Karena semua titik pada garis y = –2 dapat dituliskan ke dalam (x, –2), maka kita dapat menyatakan bahwa jarak titik (x, y) terhadap (x, –2) sama dengan jarak (x, y) terhadap (0, 2). Dengan menggunakan rumus jarak,

Sehingga, semua titik yang memenuhi kondisi tersebut adalah semua titik pada parabola dengan persamaan (1/8)x².
Lalu bagaimana jika jarak titik (x, y) terhadap fokus kurang dari jarak (x, y) terhadap direktris? Bagaimana jika jarak (x, y) terhadap fokus sama dengan 5/6 dari jarak (x, y) terhadap direktris. Mungkin kita akan menebak bahwa titik-titik (x, y) tersebut akan membentuk kurva dalam keluarga irisan kerucut lainnya. Dalam hal ini, titik tersebut akan membentuk elips. Jika jarak (x, y) terhadap fokus lebih dari jarak (x, y) terhadap direktris, maka titik-titik tersebut akan membentuk hiperbola. Pada gambar a di bawah, panjang ruas garis dari fokus ke masing-masing titik pada grafik (ditunjukkan oleh ruas garis orange), sama dengan 5/6 dari panjang ruas garis dari direktris dengan titik-titik yang sama. Perhatikan bahwa titik-titik yang memenuhi kondisi seperti itu akan membentuk setengah elips. Pada gambar b, garis-garis dan titik-titik yang membentuk setengah elips digerakkan dengan kondisi yang sama sehingga membentuk suatu grafik elips secara utuh.

Persamaan Hiperbola

Persamaan Hiperbola

Posted on 20 Januari 2014 by yos3prens

Seperti kita ketahui, hiperbola merupakan salah satu keluarga irisan kerucut yang dibentuk akibat irisan bidang yang tegak lurus dengan selimut kerucut. Suatu hiperbola memiliki 2 bagian simetris yang disebut cabang, yang terbuka ke arah yang saling berlawanan. Walaupun cabang-cabang tersebut terlihat menyerupai parabola, nantinya kita akan menginvestigasi bahwa cabang-cabang tersebut dan parabola merupakan kurva yang sangat berbeda.
Perhatikan bahwa persamaan Ax² + By² = F merupakan persamaan suatu lingkaran apabila A = B dan juga merupakan persamaan suatu elips jika A ≠ B. Dua kasus tersebut memuat penjumlahan suku-suku berderajat dua. Selanjutnya mungkin kita akan bertanya-tanya, bagaimana jika persamaannya berupa pengurangan suku-suku berderajat dua. Perhatikan persamaan 9x² – 16y² = 144. Dari persamaan tersebut kita dapat mengetahui bahwa titik pusatnya adalah titik asal (0, 0) karena tidak ada pergeseran pada variabel x dan y (a dan b keduanya adalah 0). Dengan menggunakan metode perpotongan kurva, kita dapat menggambar grafik tersebut dan menghasilkan suatu grafik hiperbola.
Contoh 1: Menggambar Grafik Hiperbola Pusat
Gambarlah grafik persamaan 9x² – 16y² = 144 dengan menggunakan perpotongan kurva dan beberapa titik tambahan jika diperlukan.
Pembahasan Dengan substitusi x = 0, kita akan menentukan perpotongan kurva tersebut dengan sumbu-y.

Karena nilai y² tidak pernah negatif, kita dapat menyimpulkan bahwa kurva tersebut tidak memiliki titik potong terhadap sumbu-y. Selanjutnya, kita substitusi y = 0 untuk menentukan titik potongnya terhadap sumbu-x.

Dengan mengetahui bahwa grafik tersebut tidak memiliki titik potong terhadap sumbu-y, kita pilih nilai x yang lebih dari 4 dan kurang dari –4 untuk membantu sketsa grafik tersebut. Dengan menggunakan x = 5 dan x = –5 menghasilkan,

Dengan memplot titik-titik yang telah kita temukan di atas kemudian menghubungkannya dengan kurva halus, dan karena kurva tersebut tidak berpotongan dengan sumbu-y, maka grafik dari persamaan yang diberikan dapat digambarkan sebagai berikut.

Karena hiperbola di atas memotong sumbu simetri horizontalnya, maka hiperbola di atas disebut sebagai hiperbola horizontal. Titik-titik (4, 0) dan (–4, 0) disebut sebagai titik-titik puncak, dan titik pusat dari hiperbola selalu berada di tengah-tengah titik puncak parabola tersebut. Jika titik pusat hiperbola berada pada titik (0, 0), maka hiperbola tersebut disebut sebagai hiperbola pusat. Sebagai catatan, titik pusat hiperbola bukan merupakan bagian dari kurva, sehingga titik pusat hiperbola di atas, titik yang berwarna biru, digambarkan sebagai titik yang terbuka. Garis yang melewati titik pusat dan titik-titik puncak hiperbola disebut sebagai sumbu transversal, sedangkan garis yang melalui titik pusat dan tegak lurus dengan sumbu transversal ini disebut sebagai sumbu konjugasi.
Pada contoh 1, koefisien dari x² merupakan bilangan yang positif kemudian dikurangkan dengan 16y²: 9x² – 16y² = 144. Hasil yang diperoleh merupakan hiperbola horizontal. Jika suku-y² positif kemudian dikurangkan dengan suku yang memuat x², hasilnya merupakan suatu hiperbola vertikal. Lebih jelasnya perhatikan gambar berikut.

About these ads

Perbedaan antara Persamaan-persamaan Lingkaran, Elips, dan Hiperbola

Perbedaan antara Persamaan-persamaan Lingkaran, Elips, dan Hiperbola

Posted on 22 Januari 2014 by yos3prens

Terdapat beberapa macam kurva dalam keluarga irisan kerucut, 3 di antaranya adalah lingkaran, elips, dan hiperbola. Pada contoh berikut, kita akan mengidentifikasi jenis kurva apa yang dibentuk oleh persamaan-persamaan yang diberikan, tanpa melukis grafik persamaannya. Seperti yang akan kita ketahui, jenis-jenis persamaan yang bersesuaian akan memiliki karakteristik tertentu yang dapat membantu kita untuk membedakan antara persamaan satu dengan persamaan lainnya.
Contoh: Mengidentifikasi Irisan Kerucut dari Persamaannya
Identifikasi masing-masing persamaan berikut apakah merupakan persamaan lingkaran, elips, ataukah hiperbola. Berikan alasanmu dan tentukan titik pusatnya, tetapi jangan menggambar grafik-grafiknya.

1. y² = 36 + 9x²
2. 4x² = 16 – 4y²
3. x² = 225 – 25y²
4. 25x² = 100 + 4y²
5. 3(x – 2)² + 4(y + 3)² = 12
6. 4(x + 5)² = 36 + 9(y – 4)²

Pembahasan

1. Dengan menulis persamaannya menjadi y² – 9x² = 36, kita memperoleh a = 0 dan b = 0. Karena persamaan tersebut memuat selisih suku-suku berderajat dua, maka persamaan tersebut merupakan persamaan hiperbola (vertikal). Titik pusat dari hiperbola tersebut adalah (0, 0).
2. Kita tulis kembali persamaan tersebut menjadi 4x² + 4y² = 16, kemudian membagi kedua ruas dengan 4, maka kita akan memperoleh persamaan x² + y² = 4. Persamaan tersebut merupakan persamaan lingkaran berjari-jari 2 dan memiliki titik pusat di (0, 0).
3. Persamaan x² = 225 – 25y² dapat ditulis menjadi x² + 25y² = 225. Persamaan tersebut terdiri dari penjumlahan suku-suku berderajat dua yang memiliki koefisien berbeda. Sehingga, persamaan tersebut merupakan persamaan elips yang memiliki titik pusat di (0, 0).
4. Dengan menulis kembali persamaan yang diberikan menjadi 25x² – 4y² = 100, kita dapat melihat persamaan tersebut memuat pengurangan suku-suku berderajat dua. Sehingga, persamaan tersebut merupakan persamaan dari hiperbola (horizontal) dengan titik pusat di (0, 0).
5. Persamaan yang diberikan memiliki bentuk pemfaktoran dan memuat penjumlahan suku-suku berderajat dua dengan koefisien yang berbeda. Persamaan ini merupakan persamaan suatu elips dengan titik pusat di (2, –3).
6. Setelah kita tulis kembali persamaan yang diberikan menjadi 4(x + 5)² – 9(y – 4)² = 36, kita dapat mengamati bahwa persamaan tersebut memuat pengurangan suku-suku berderajat dua yang memiliki koefisien berbeda. Sehingga, persamaan tersebut merupakan persamaan suatu hiperbola horizontal dengan titik pusat di (–5, 4).

FAKTOR-FAKTOR PERSEKUTUAN DAN FPB

 FAKTOR-FAKTOR PERSEKUTUAN DAN FPB

Andi memiliki 12 buah apel dan 18 buah jeruk. Dia berencana untuk membagikan buah-buah tersebut secara rata kepada temannya. Yang dimaksud rata di sini adalah bahwa temannya akan mendapatkan buah apel dan buah jeruk yang banyaknya sama dengan temannya yang lain. Ada berapa banyak teman Andi yang akan menerima buah-buahan tersebut? Berapa banyak teman Andi maksimal yang akan menerima buah-buahan tersebut?

Kemungkinan pertama, Andi dapat memberikan buah-buahan tersebut kepada seorang temannya. Sehingga temannya tersebut akan mendapatkan 12 buah apel dan 18 buah jeruk. Kemungkinan ini merupakan kemungkinan yang paling sederhana. Kemungkinan kedua, Andi dapat memberikan buah-buahan tersebut kepada 2 orang temannya. Sehingga masing-masing temannya akan mendapatkan 12 : 2 = 6 buah apel dan 18 : 2 = 9 buah jeruk.
Apakah Andi dapat membagikan buah-buahannya tersebut secara rata kepada 4 orang temannya? Tentu tidak. Buah apel yang berjumlah 12 memang dapat dibagi dengan 4, akan tetapi banyaknya buah jeruk, yaitu 18, apabila dibagi dengan 4 sama dengan 4 dan sisa 2. Atau dengan kata lain, 18 dibagi 4 tidak menghasilkan suatu bilangan bulat. Ini dapat dikatakan bahwa 4 merupakan faktor dari 12, tetapi bukan faktor dari 18. Apakah yang dimaksud faktor suatu bilangan?

Faktor suatu bilangan adalah suatu bilangan yang dapat habis membagi bilangan tersebut.

Mari kita kembali kepada permasalahan di awal. Ada berapa banyak teman Andi yang akan menerima buah-buahan tersebut? Untuk menjawab pertanyaan ini, mari kita daftar semua faktor dari 12 dan 18. Semua faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12. Sedangkan semua faktor dari 18 adalah 1, 2, 3, 6, 9, dan 18. Kedua bilangan 12 dan 18 memiliki faktor-faktor yang sama, yaitu 1, 2, 3, dan 6. Faktor-faktor yang sama tersebut disebut faktor persekutuan.

Faktor persekutuan adalah faktor-faktor yang sama dari dua bilangan atau lebih.

Banyaknya teman Andi yang akan diberikan buah harus dapat membagi bilangan 12 maupun 18. Sehingga banyaknya teman Andi haruslah faktor-faktor persekutuan dari 12 dan 18, yaitu 1, 2, 3, dan 6.
Selanjutnya mari kita lihat pertanyaan lainnya. Berapa banyak teman Andi maksimal yang akan menerima buah-buahan tersebut? Karena banyaknya teman Andi haruslah 1, 2, 3, dan 6, maka banyaknya teman Andi maksimal adalah 6 orang. Enam merupakan bilangan terbesar dari faktor-faktor persekutuan dari 12 dan 18. Hal ini dapat dikatakan bahwa 6 merupakan faktor persekutuan terbesar (FPB) dari 12 dan 18.

Faktor persekutuan terbesar (FPB) adalah faktor persekutuan yang nilainya terbesar di antara faktor-faktor persekutuan lainnya.

Setelah mengenal faktor, faktor persekutuan, dan FPB, mari kita lanjutkan pembahasan kita menuju bagaimana cara menentukan FPB dari dua bilangan atau lebih. Untuk menentukan FPB dari dua bilangan atau lebih, kita dapat menggunakan cara mendaftar, faktorisasi prima, dan sengkedan.
Menentukan FPB dengan Cara Mendaftar
Misalkan kita akan menentukan FPB dari 24 dan 32. Pertama, kita daftar semua faktor dari 24 dan 32. Semua faktor dari 24 dan 32 dapat ditentukan dengan menggunakan tabel berikut.

Dari tabel tersebut kita dapat memperoleh bahwa faktor persekutuan dari 24 dan 32 adalah 1, 2, 4, dan 8. Sehingga FPB dari 24 dan 32 adalah 8.
Menentukan FPB dengan Faktorisasi Prima
Misalkan kita akan menentukan FPB dari 140 dan 250. Pertama, kita tulis 140 dan 250 dalam perkalian faktor-faktor primanya. Faktor-faktor prima dari 140 dan 250 dapat dicari dengan menggunakan pohon faktor.

Dari pohon faktor di atas dapat diperoleh,
140 = 2² × 5 × 7
250 = 2 × 5³
Setelah mengubah bilangan-bilangan 140 dan 250 ke dalam perkalian faktor-faktor primanya, selanjutnya kita tentukan FPB-nya. Bagaimana caranya?

FPB dari dua bilangan dapat ditentukan dengan mengalikan faktor persekutuan prima dengan pangkat terendah.

Faktor persekutuan prima dari 140 dan 250 adalah 2 dan 5. Faktor prima 2 dari 140 berpangkat 2, sedangkan faktor prima 2 dari 250 berpangkat 1. Kita pilih yang pangkatnya terendah, yaitu 2 pangkat 1. Demikian juga dengan faktor prima 5 dari 140 dan 250, kita pilih faktor yang pangkatnya terendah, yaitu 5 pangkat 1. Sehingga FPB dari 140 dan 250 adalah 2 × 5 = 10.
Menentukan FPB dengan Cara Sengkedan
Pada contoh-contoh sebelumnya kita menentukan FPB dari 2 bilangan. Sekarang kita akan menentukan FPB dari 3 bilangan, yaitu 18, 24, dan 30. FPB dari 18, 24, dan 30 dapat ditentukan dengan cara sengkedan sebagai berikut.

Aturan dari cara sengkedan adalah sebagai berikut:

1. Tuliskan bilangan-bilangan yang akan ditentukan FPB-nya secara mendatar.
2. Carilah bilangan prima yang dapat membagi sebagian atau seluruh bilangan tersebut. Untuk mencari bilangan prima ini, sebaiknya pilih bilangan prima dari yang terkecil: 2, 3, 5, dan seterusnya.
3. Apabila bilangan prima pembagi yang dipilih dapat membagi semua bilangan, lingkarilah bilangan prima tersebut. Tuliskan hasil baginya di baris bawah bilangan yang dibagi.
4. Apabila ada bilangan yang tidak habis dibagi oleh bilangan prima pembagi, tuliskan kembali bilangan tersebut di baris bawahnya.
5. Lakukan terus menerus hingga mendapatkan suatu baris yang hanya berisi bilangan 1.
6. FPB dari bilangan-bilangan yang dicari adalah perkalian semua bilangan prima pembagi yang dilingkari.

Dari contoh di atas, kita memperoleh bahwa bilangan prima pembagi yang dilingkari adalah 2 dan 3. Sehingga FPB dari 18, 24, dan 30 adalah 2 × 3 = 6.
Setelah kita berlatih menentukan FPB dari 2 atau 3 bilangan di atas, selanjutnya kita akan mencoba untuk menyelesaikan permasalahan berikut.
Pemecahan Masalah
Bilangan-bilangan 3.154, 17.328, dan 11.027 dibagi dengan bilangan yang sama sisanya berturut-turut adalah 4, 3, dan 2. Berapa bilangan pembagi terbesar yang mungkin?

PERKALIAN PECAHAN

 PERKALIAN PECAHAN

Untuk mengikuti lomba memasak, Indira dan kelompoknya diwajibkan membawa bahan-bahan untuk memasak. Dalam kelompok Indira tersebut, Indira dan seorang temannya, Mawar, ditugasi temannya untuk membawa beras dua pertiga kilogram. Indira dan Mawar sepakat bahwa masing-masing dari mereka akan membawa setengah dari beras tersebut. Berapa kilogram beras yang akan dibawa oleh Indira?
Untuk menjawab permasalahan tersebut, kita dapat menggunakan operasi perkalian pada pecahan. Indira akan membawa setengah dari dua pertiga kilogram beras, yang dapat dituliskan 1/2 × 2/3 kg. Berapakah hasil kali 1/2 dan 2/3? Untuk menjawabnya, kita dapat menggunakan konsep luas persegi panjang sebagai berikut.

Perhatikan persegi panjang warna hijau! Persegi panjang tersebut memiliki panjang 2/3 dan lebar 1/2. Dari gambar di atas, dengan jelas kita dapat mengetahui bahwa luas dari persegi panjang tersebut adalah 2/6 bagian dari persegi satuan. Karena luas persegi panjang adalah panjang dikali lebar, maka kita dapat memperoleh 2/3 × 1/2 = 2/6. Sehingga, beras yang akan dibawa oleh Indira adalah 2/6 atau 1/3 kg.
Apa yang dapat kita simpulkan dari permasalahan di atas? Sebelum kita masuk ke kesimpulan, perhatikan beberapa contoh perkalian pecahan lainnya berikut.

Dari gambar 1 kita dapat memperoleh bahwa 2/5 dikali 3/4 sama dengan 6/20. Pada gambar 2, 7/8 dikali dengan 3/4 sama dengan 21/32. Sedangkan pada gambar 3, kita dapat memperoleh bahwa 4/6 dikali dengan 5/6 sama dengan 20/36. Ketiga perkalian pecahan di atas dapat dituliskan sebagai berikut.

Apa yang dapat kita amati dari perkalian di atas? Bagaimana dengan pembilang dan penyebut dari pecahan hasil perkalian? Pada perkalian pertama, pembilang dari hasil perkaliannya adalah 6, yang sama dengan 2 × 3, yaitu perkalian dari pembilang pecahan-pecahan yang dikalikan. Sedangkan penyebut dari hasil perkaliannya adalah 20, yang sama dengan 5 × 4, yaitu perkalian dari penyebut pecahan-pecahan yang dikalikan. Demikian juga pada operasi perkalian kedua dan ketiga.

Hasil kali dua pecahan merupakan pecahan yang pembilang dan penyebutnya secara berturut-turut merupakan perkalian dari pembilang dan penyebut pecahan-pecahan yang dikalikan.

Untuk lebih memahami mengenai perkalian pecahan, perhatikan beberapa contoh berikut.

Bagaimana dengan perkalian yang melibatkan bilangan asli atau pecahan campuran? Untuk kasus ini, kita harus mengubah bilangan asli dan pecahan campuran tersebut ke dalam pecahan biasa. Perhatikan contoh berikut!

PENGURANGAN PECAHAN

 PENGURANGAN PECAHAN

Dalam suatu upacara bendera, Dewi, Cecil, dan Rahma berada dalam satu barisan. Dewi berada paling depan, Cecil 1/4 dam di belakang Dewi, sedangkan Rahma berada 3/4 dam di belakang Dewi. Dapatkah kita menentukan jarak Cecil dengan Rahma? Untuk menjawabnya, pertama-tama perhatikan gambar berikut!

Dari gambar di atas, kita dapat memperoleh bahwa jarak antara Cecil dengan Rahma adalah 2 bagian dari 4 dekameter. Atau dengan kata lain, tiga perempat dikurangi seperempat sama dengan dua perempat. Pernyataan tersebut apabila dituliskan dalam bentuk pecahan akan menjadi seperti berikut.

Apabila kita perhatikan, operasi pengurangan pada pecahan memiliki aturan yang sama dengan operasi penjumlahan, yaitu pembilang dikurangi dengan pembilang, sedangkan penyebutnya tetap. Operasi pengurangan di atas dapat kita lengkapi sebagai berikut.

Bagaimana dengan operasi pengurangan pada pecahan-pecahan yang memiliki penyebut yang berbeda? Ya, seperti pada operasi penjumlahan, kita harus menyamakan penyebut dari pecahan-pecahan tersebut menjadi KPK-nya sebelum melakukan operasi pengurangan. Perhatikan beberapa contoh berikut!

Pengurangan pecahan di atas dapat dimodelkan oleh gambar berikut.

Dari uraian di atas, apakah kamu sudah memahami operasi pengurangan pada pecahan? Okay, kalau sudah, sekarang waktunya untuk menyelesaikan permasalahan berikut.
Pemecahan Masalah
Perhatikan garis bilangan berikut!

Dengan menggeser garis bilangan tersebut ke kiri atau ke kanan, tentukan hasil dari 3/4 – 1/2!